2017年高考数学复数必考知识点

2017-04-15

高中数学常考知识点之复数定义

我们把形如a+bi(a,b均为实数)的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。当虚部等于零时，这个复数可以视为实数;当z的虚部不等于零时，实部等于零时，常称z为纯虚数。复数域是实数域的代数闭包，也即任何复系数多项式在复数域中总有根。

高中数学常考知识点之复数表达式

虚数是与任何事物没有联系的，是绝对的，所以符合的表达式为：

a=a+ia为实部，i为虚部

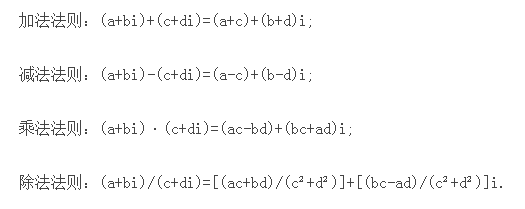
例如：[(a+bi)+(c+di)]-[(a+c)+(b+d)i]=0，最终结果还是0，也就在数字中没有复数的存在。[(a+bi)+(c+di)]-[(a+c)+(b+d)i]=z是一个函数。

①几何形式

复数z=a+bi被复平面上的点z(a，b)唯一确定。这种形式使复数的问题可以借助图形来研究。也可反过来用复数的理论解决一些几何问题。

②向量形式

复数z=a+bi用一个以原点O(0,0)为起点，点Z(a,b)为终点的向量OZ表示。这种形式使复数四则运算得到恰当的几何解释。

③三角形式

复数z=a+bi化为三角形式

加法法则

复数的加法按照以下规定的法则进行:设z1=a+bi,z2=c+di是任意两个复数，

则它们的和是(a+bi)+(c+di)=(a+c)+(b+d)i

两个复数的和依然是复数，它的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。

复数的加法满足交换律和结合律，

即对任意复数z1,z2,z3,有

减法法则

复数的减法按照以下规定的法则进行:设z1=a+bi,z2=c+di是任意两个复数，

则它们的差是

两个复数的差依然是复数，它的实部是原来两个复数实部的差，它的虚部是原来两个虚部的差。

乘法法则

规定复数的乘法按照以下的法则进行

设z1=a+bi，z2=c+di(a、b、c、d∈R)是任意两个复数，那么它们的积

其实就是把两个复数相乘，类似两个多项式相乘，展开得: ac+adi+bci+bdi^2，因为i^2=-1，所以结果是(ac-bd)+(bc+ad)i 。两个复数的积仍然是一个复数。

除法法则

复数除法定义:满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商

运算方法:可以把除法换算成乘法做,在分子分母同时乘上分母的共轭. 所谓共轭你可以理解为加减号的变换,互为共轭的两个复数相乘是个实常数

除法运算规则

于是有:(a+bi)/(c+di)=(ac+bd)/(c^2+d^2) +(bc-ad)/(c^2+d^2)i②利用共轭复数将分母实数化得(见右图

点评:①是常规方法

②是利用初中我们学习的化简无理分式时，都是采用的分母有理化思想方法，而复数c+di与复数c-di，相当于我们初中学习的的对偶式，它们之积为1是有理数，而(c+di)·(c-di)=c2+d2是正实数.所以可以分母实数化. 把这种方法叫做分母实数化法。