角平分线的定义角平分线的定义是什么

2017-05-23

角平分线的定义

角平分线定义(Anglebisectordefinition)从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线(bisectorofangle)。三角形三条角平分线的交点叫做三角形的内心。三角形的内心到三边的距离相等，是该三角形内切圆的圆心。其它解释：角平分线是在角的型内及形上，到角两边距离相等的点的轨迹。

角平分线的性质

在角的平分线上的点到这个角的两边的距离相等。

(逆定理)在一个角的内部(包括顶点)且到角的两边的距离相等的点在这个角的角平分线上。

三角形的角平分线定义

三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线(也叫三角形的内角平分线)。由定义可知，三角形的角平分线是一条线段。由于三角形有三个内角，所以三角形有三条角平分线。三角形的角平分线交点一定在三角形内部。

角平分线的其它解释

角平分线可以看作是到角两边距离相等的所有点的集合。

三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线(也叫三角形的内角平分线)。由定义可知，三角形的角平分线是一条线段。由于三角形有三个内角，所以三角形有三个角平分线。三角形的角平分线交点一定在三角形内部。

角平分线的作法

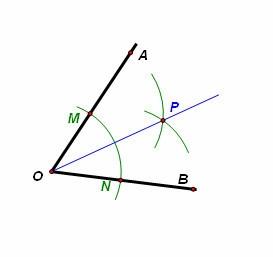
在角AOB中，画角平分线

方法一：1.以点O为圆心，以任意长为半径画弧，两弧交角AOB两边于点M，N。

2.分别以点M，N为圆心，以大于1/2MN的长度为半径画弧，两弧交于点P。

3.作射线OP。

则射线OP为角AOB的角平分线。

证明：连接PM,PN

在△POM和△PON中

∵OM=ON,PM=PN,PO=PO

∴△POM≌△PON(SSS)

∴∠POM=∠PON，即射线OP为角AOB的角平分线

当然，角平分线的作法有很多种。下面再提供一种尺规作图的方法供参考。

方法二：1.在两边OA、OB上分别截取OM、OC和ON、OD，且使得OM=ON，OC=OD;

2.连接CN与DM，他们相交于点P;

3.作射线OP。

则射线OP为角AOB的角平分线。

角平分线的举例

求证：三角形内角平分线分对边所得的两条线段和这个角的两边对应成比例。

如图，若AD是△ABC的角平分线，则 BD/DC=AB/AC 。

证明：作CE∥AD交BA延长线于E。

∵CE∥AD

∴△BDA∽△BCE

∴BA/BE=BD/BC

∴ BA/AE=BD/DC

∵CE∥AD

∴∠BAD=∠E,∠DAC=∠ACE

∵AD平分∠BAC

∴∠BAD=∠CAD

∴ ∠BAD=∠CAD=∠ACE=∠E

即∠ACE=∠E

∴ AE=AC

又∵BA/AE=BD/DC

∴BA/AC=BD/DC

(注：例题中∵、∴分别表示为因为、所以)

角平分线的判断

角的内部到角的两边距离相等的点，都在这个角的平分线上。

判定定理的证明：如图，已知PD⊥OA于D，PE⊥OB于E，且PD=PE，求证：OC平分∠AOB

证明：在Rt△OPD和Rt△OPE中：

OP=OP，PD=PE

∴Rt△OPD≌Rt△OPE(HL)

∴∠1=∠2

∴ OC平分∠AOB

猜你感兴趣：

1.人教版八年级数学上册第2课时角平分线的判定精选练习题

2.八年级数学上册角平分线的性质精选练习题

3.八年级数学上册三角的线与角平分线精选练习题

角平分线的定义角平分线的定义是什么

相关话题