2016全国卷3文科数学真题-2016全国卷3文科数学答案（选择填空题

全国卷三适用于海南这些省份，下面是小编给大家整理的2016全国卷3文科数学真题和选择题和填空题部分答案，真题有图片版和文字版，方便大家对照。

2016全国卷3文科数学真题图片版

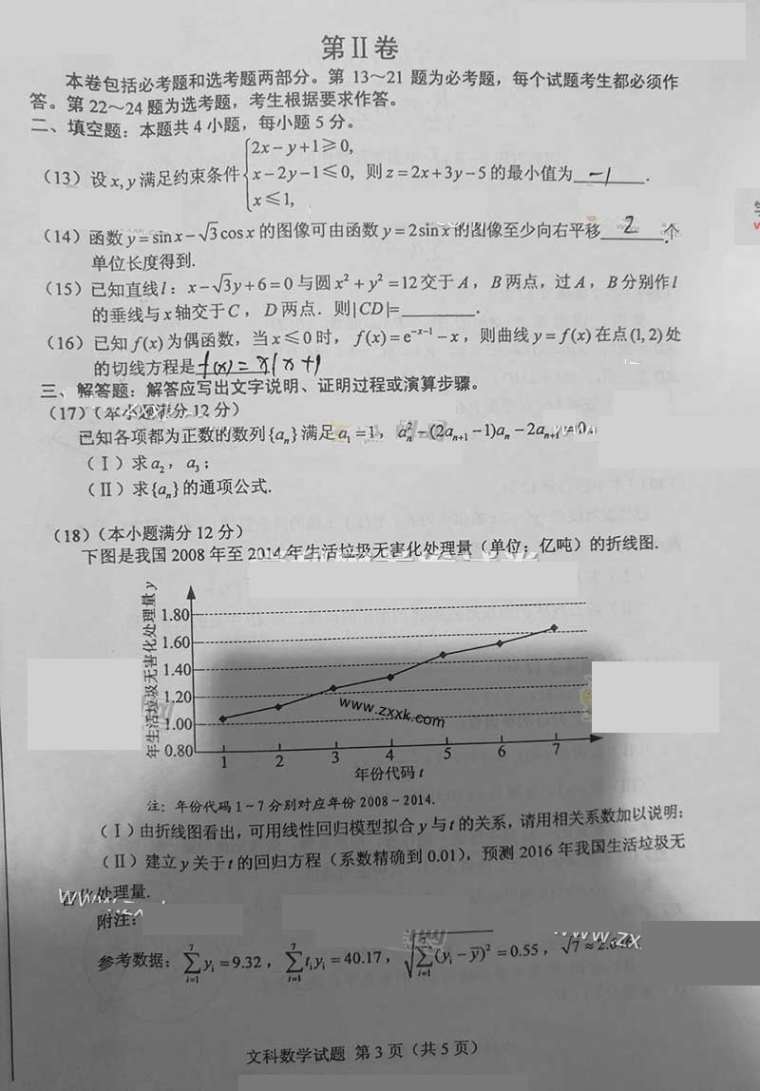
2016全国卷3文科数学真题答案(选择题，填空题)

2016全国卷3文科数学真题文字版

注意事项：

1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页，第Ⅱ卷3至5页.

2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置.

3.全部答案在答题卡上完成，答在本试题上无效.

4.考试结束后，将本试题和答题卡一并交回.

第Ⅰ卷

一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.

(1)设集合S=S={xP(x-2)(x-3)≥0}，T={xIx>0}则SIT=

(A)[2，3](B)(-∞，2][3,+∞)

(C)[3,+∞)(D)(0，2][3,+∞)

(2)若z=1+2i，则

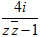
(A)1(B)-1(C)i(D)-i

(3)已知向量

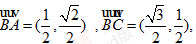
,则ABC=

(A)30°(B)45°(C)60°(D)120°

(4)某旅游城市为向游客介绍本地的气温情况，绘制了一年中月平均最高气温和平均最低气温的雷达图。图中A点表示十月的平均最高气温约为15℃，B点表示四月的平均最低气温约为5℃。下面叙述不正确的是

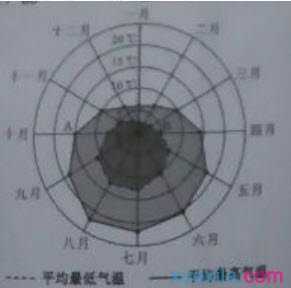
(A)各月的平均最低气温都在0℃以上

(B)七月的平均温差比一月的平均温差大

(C)三月和十一月的平均最高气温基本相同

(D)平均气温高于200C的月份有5个

(5)若

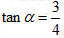
，则

=

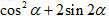
(6)已知

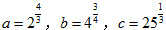
，则

(A)b

(7)执行下图的程序框图，如果输入的a=4，b=6，那么输出的n=

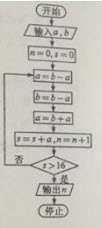
(A)3

(B)4

(C)5

(D)6

(8)在△ABC中，

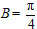
，BC边上的高等于,则

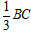
cosA=

(9)如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为

(A)

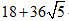
(B)

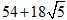
(C)90

(D)81

(10)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球，若ABBC，AB=6，BC=8，AA1=3，则V的最大值是

(A)4π(B)

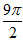
(C)6π(D)

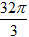
(11)已知O为坐标原点，F是椭圆C：

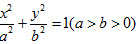
的左焦点，A，B分别为C的左，右顶点.P为C上一点，且PF⊥x轴.过点A的直线l与线段PF交于点M，与y轴交于点E.若直线BM经过OE的中点，则C的离心率为

(12)定义“规范01数列”{an}如下：{an}共有2m项，其中m项为0，m项为1，且对任意k≤2m，a1,a2,...ak中0的个数不少于1的个数.若m=4，则不同的“规范01数列”共有

(A)18个(B)16个(C)14个(D)12个

第II卷

本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答.第(22)题~第(24)题为选考题，考生根据要求作答.

二、填空题：本大题共3小题，每小题5分

(13)若x，y满足约束条件

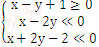
则z=x+y的最大值为_____________. (14)函数

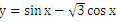
的图像可由函数

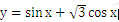
的图像至少向右平移_____________个单位长度得到。

(15)已知f(x)为偶函数，当x<0时，f(x)=ln(-x)+3x，则曲线y=f(x)，在带你(1，-3)处的切线方程是_______________。

(16)已知直线l:mx+y+3m-

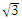
与圆x2+y2=12交于A，B两点，过A，B分别做l的垂线与x轴交于C，D两点，若|AB|=2

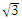
，则|CD|__________________.

三.解答题：解答应写出文字说明，证明过程或演算步骤.

(17)(本小题满分12分)

已知数列{an}的前n项和Sn=1+a，Sn=1+λan，其中λ≠0

(I)证明{an}是等比数列，并求其通项公式

(II)若S5=

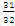
，求λ

(18)(本小题满分12分)

下图是我国2008年至2014年生活垃圾无害化处理量(单位：亿吨)的折线图

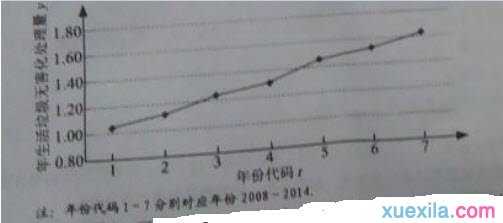
(I)由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明

(II)建立y关于t的回归方程(系数精确到0.01)，预测2016年我国生活垃圾无害化处理量。

(19)(本小题满分12分)

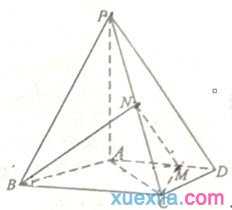
如图，四棱锥P-ABCD中，PA⊥地面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.

(I)证明MN∥平面PAB;

(II)求直线AN与平面PMN所成角的正弦值.

(20)(本小题满分12分)

已知抛物线C：的焦点为F，平行于x轴的两条直线分别交C于A，B两点，交C的准线于P，Q两点.

(I)若F在线段AB上，R是PQ的中点，证明AR∥FQ;

(II)若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程.

(21)(本小题满分12分)

设函数f(x)=acos2x+(a-1)(cosx+1)，其中a>0，记的最大值为A.

(Ⅰ)求f'(x);

(Ⅱ)求A;

(Ⅲ)证明|f'(x)|≤2A.

请考生在[22]、[23]、[24]题中任选一题作答。作答时用2B铅笔在答题卡上把所选题目题号后的方框涂黑。如果多做，则按所做的第一题计分。

22.(本小题满分10分)选修4-1：几何证明选讲

如图，⊙O中□AB的中点为P，弦PC，PD分别交AB于E，F两点.

(I)若∠PFB=2∠PCD，求∠PCD的大小;

(II)若EC的垂直平分线与FD的垂直平分线交于点G，证明OG⊥CD.

23.(本小题满分10分)选修4-4：坐标系与参数方程

在直角坐标系xOy中，曲线C1的参数方程为

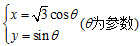
，以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为

.

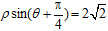
(I)写出C1的普通方程和C2的直角坐标方程;

(II)设点P在C1上，点Q在C2上，求|PQ|的最小值及此时P的直角坐标.

24.(本小题满分10分)选修4-5：不等式选讲

已知函数

(I)当a=2时，求不等式的解集;

(II)设函数当时，f(x)+g(x)≥3，求a的取值范围.