高三数学概率与统计专题训练试题及答案
考试是检测学习成效的重要手段,孰能生巧,考前一定要多做多练,高三数学概率与统计复习的如何呢?以下是小编为大家收集整理的高三数学概率与统计专题训练试题,请考生认真复习!
高三数学概率与统计专题训练试题
1.(2014·保定调研)近年来,我国的高铁技术发展迅速,铁道部门计划在A、B两城之间开通高速列车,假设在试运行期间,每天8:00-9:00,9:00-10:00两个时段内各发一趟列车由A城到B城(两车发生情况互不影响),A城发车时间及其概率如下表所示:
发生时间
8:10
8:30
8:50
9:10
9:30
9:50
概率
61
21
31
61
21
31
若甲、乙两位旅客打算从A城到B城,假设他们到达A城火车站侯车的时间分别是周六8:00和周日8:20.(只考虑候车时间,不考虑其他因素)
(1)设乙侯车所需时间为随机变量X,求X的分布列和数学期望;
(2)求甲、乙二人候车时间相等的概率.
解 (1)X的所有可能取值为10、30、50、70、90(分钟),其概率分布列如下
X
10
30
50
70
90
P
21
31
361
121
181
X的数学期望E(X)=10×2(1)+30×3(1)+50×36(1)+70×12(1)+90×18(1)=9(245)(分钟).
(2)甲、乙二人候车时间分别为10分钟、30分钟、50分钟的概率为
P甲10=6(1),P甲30=2(1),P甲50=3(1);
P乙10=2(1),P乙30=3(1),P乙50=6(1)×6(1)=36(1).
所以所求概率P=6(1)×2(1)+2(1)×3(1)+3(1)×36(1)=108(28)=27(7),
即甲、乙二人候车时间相等的概率为27(7).
2.(2014·皖南八校联考)从正方体的各个表面上的12条面对角线中任取2条,设ξ为2条面对角线所成的角(用弧度制表示),如当2条面对角线垂直时,ξ=2(π).
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
解 (1)当ξ=0时,即所选的2条面对角线平行,则P(ξ=0)=12(2)=11(1).
(2)ξ的可能取值为0,3(π),2(π).
则P(ξ=0)=12(2)=11(1),P3(π)=12(2)=11(8),P2(π)=12(2)=11(2).
ξ的分布列如下:
ξ
3π
2π
P
111
118
112
E(ξ)=0×11(1)+3(π)×11(8)+2(π)×11(2)=3(π).
3.(2014·广州调研)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:
PM2.5日均浓度
0~35
35~75
75~115
115~150
150~250
>250
空气质量类别
优
良
轻度污染
中度污染
重度污染
严重污染
从甲城市2014年9月份的30天中随机抽取15天的PM2.5日均浓度指数数据茎叶图如图所示.
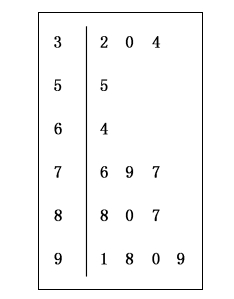
(1)试估计甲城市在2014年9月份30天的空气质量类别为优或良的天数;
(2)在甲城市这15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
解 (1)由茎叶图可知,甲城市在2014年9月份随机抽取的15天中的空气质量类别为优或良的天数为5.
所以可估计甲城市在2014年9月份30天的空气质量类别为优或良的天数为10.
(2)X的所有可能取值为0,1,2,
因为P(X=0)=15(2)=7(3),P(X=1)=15(2)=21(10),P(X=2)=15(2)=21(2),
所以X的分布列为:
X
1
2
P
73
2110
212
数学期望E(X)=0×7(3)+1×21(10)+2×21(2)=3(2).
4.(2014·浙江名校联考)甲、乙两支球队进行总决赛,比赛采用七场四胜制,即若有一队先胜四场,则此队为总冠军,比赛结束.因两队实力相当,每场比赛两队获胜的可能性均为2(1).据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
(1)求总决赛中获得门票总收入恰好为300万元的概率;
(2)设总决赛中获得门票总收入为X,求X的均值E(X).
解 (1)依题意,每场比赛获得的门票收入组成首项为40,公差为10的等差数列.
设此数列为{an},则易知a1=40,an=10n+30,
所以Sn=2(n(10n+70))=300.
解得n=-12(舍去)或n=5,
所以总决赛共比赛了5场.
则前4场比赛中,一支球队共赢了3场,且第5场比赛中,领先的球队获胜,其概率为C4(1)2(1)4=4(1).
(2)随机变量X可取的值为S4,S5,S6,S7,即220,300,390,490.
又P(X=220)=2×2(1)4=8(1),
P(X=300)=C4(1)2(1)4=4(1),
P(X=390)=C5(2)2(1)5=16(5),
P(X=490)=C6(3)2(1)6=16(5),
所以X的分布列为
X
220
300
390
490
P
81
41
165
165
所以X的均值E(X)=377.5(万元).
5.自驾游从A地到B地有甲、乙两条线路,甲线路是A-C-D-B,乙线路是A-E-F-G-H-B,其中CD段、EF段、GH段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表1所示.经调查发现,堵车概率x在,1(2)上变化,y在2(1)上变化.在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计CD段平均堵车时间,调查了100名走甲路线的司机,得到表2数据.
CD段
EF段
GH段
堵车概率
x
y
41
平均堵车时间(单位:小时)
a
2
1
堵车时间(单位:小时)
频数
[0,1]
8
(1,2]
6
(2,3]
38
(3,4]
24
(4,5]
24
(1)求CD段平均堵车时间a的值;
(2)若只考虑所花汽油费期望值的大小,为了节约,求选择走甲线路的概率.
解 (1)a=2(1)×100(8)+2(3)×100(6)+2(5)×100(38)+2(7)×100(24)+2(9)×100(24)=3.
(2)设走甲线路所花汽油费为ξ元,则E(ξ)=500(1-x)+(500+60)x=500+60x.
设走乙线路多花的汽油费为η元,
∵EF段与GH段堵车与否相互独立,
∴P(η=0)=(1-y)×4(1),
P(η=20)=(1-y)×4(1),
P(η=40)=y×4(1),
P(η=60)=4(1)y,
∴E(η)=0×(1-y)×4(1)+20×(1-y)×4(1)+40×y×4(1)+60×4(1)y=40y+5.
∴走乙线路所花的汽油费的数学期望为E(545+η)=545+E(η)=550+40y.
依题意,选择走甲线路应满足(550+40y)-(500+60x)≥0,
即6x-4y-5≤0,又3(2)<x<1,0<y<2(1),
∴P(选择走甲线路)=2(1)=8(7).