高一数学线面、面面垂直的判定知识点复习

线面、面面垂直垂直关系是高中数学的重要内容之一，线面、面面垂直垂直关系知识点有哪些呢?下面是小编为大家整理的高一数学必修2线面、面面垂直的判定知识点复习资料，希望对大家有所帮助!

一、 高一数学必修2线面、面面垂直的判定知识点复习

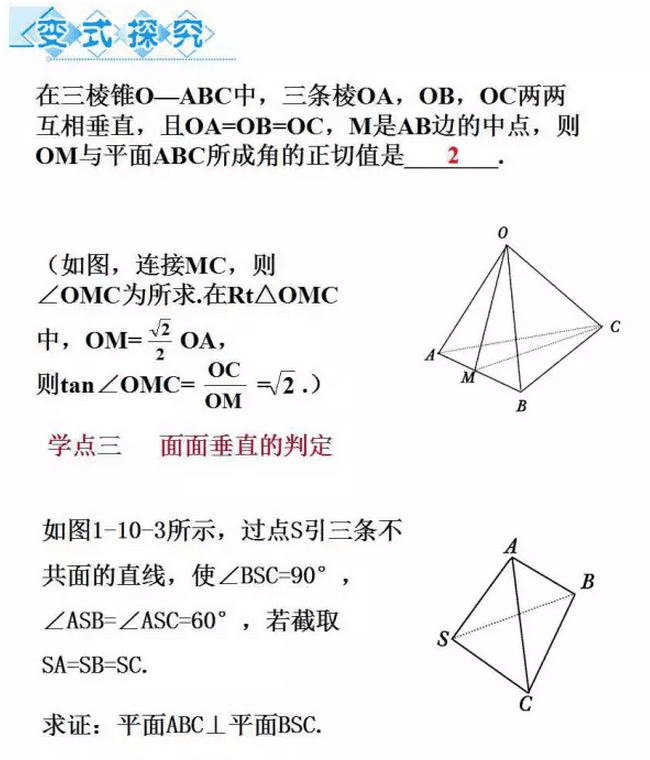
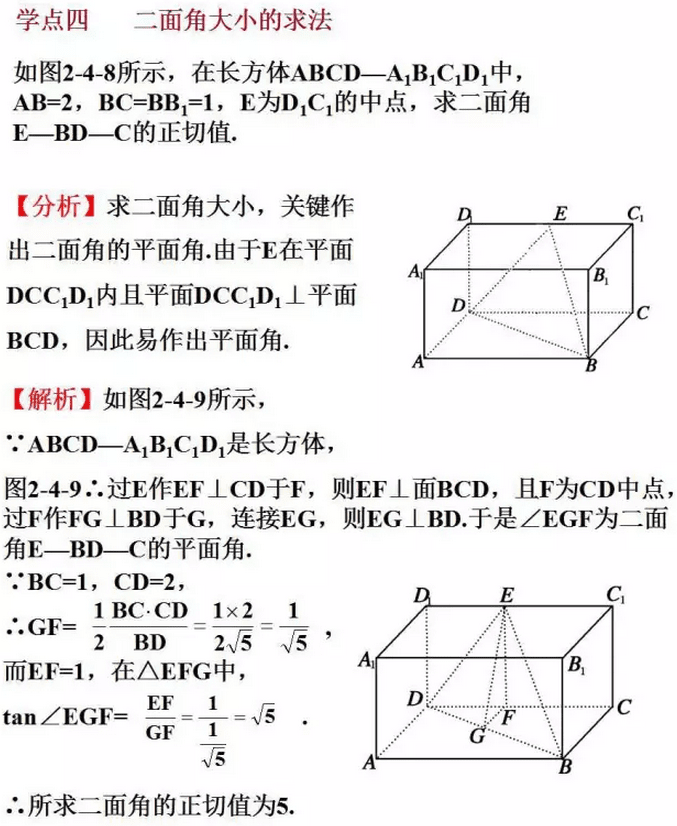
二、高一数学必修2线面、面面垂直的判定重难点分析

1.怎样理解线面垂直的判定定理?

直线和平面垂直的判定定理，应抓住“两条”和“相交”这两个关键词语.要判断一条已知直线和一个平面是否垂直，取决于在这平面内能否找出两条相交直线和已知直线垂直，至于这两条相交直线是否和已知直线有公共点，是无关紧要的.

2.怎样理解直线和平面所成的角?

直线和平面所成的角问题中主要是斜线和平面所成角问题.斜线和平面所成角的定义中给出了求解斜线和平面所成角的步骤：

①确定斜线和平面的交点(即斜足);

②经过斜线上除斜足以外的任意一点作平面的垂线，从而确定斜线的射影;

③由垂线段、斜线段及其射影构成的直角三角形，

通过解此三角形，得到斜线和平面所成的角，同

时要注意直线和平面所成角的范围.

在求解斜线和平面所成角的过程中，确定点在直线上或平面上的射影是关键，确定点在平面上射影位置有以下几种方法：

①斜线上任意一点在平面上的射影必在斜线在平面上的射影上;

②利用垂直关系得出线面垂直，确定射影.

3.如何用两平面垂直的定义证明平面与平面垂直?

两平面垂直实际上是由直线与平面垂直和线线垂直来定义的，利用这个定义可直接证明两平面垂直，其步骤为：

(1)找到两个相交平面α,β的交线a及这两个平面与第三个平面γ相交所得到的两条交线b,c;

(2)证明a⊥γ,b⊥c;

(3)根据定义，得到α⊥β.

4.在二面角的学习中应注意什么问题?

(1)二面角的平面角的概念应注意强调:顶点在二面角的棱上,两条边分别在二面角的两个面内,且这两条边都垂直于二面角的棱,这样选取的角的大小与角的位置的选取无关.

(2)画二面角的平面角时,使平面角的两边分别平行于

表示两个半平面的平行四边形的一组对边,即表明垂

直于二面角的棱,平面角∠AOB的大小与D点的位置

无关.

(3)二面角的计算方法:

①定义.作二面角的平面角——在棱上取一点,分别在两个面内作棱的垂线,这两条射线组成二面角的平面角.利用定义作二面角的平面角,关键在于找棱及棱上的特殊点.学习时要特别注意平移和补形方法的灵活运用.

②用垂面法.作二面角的平面角——作垂直于二面角的棱或二面角的两个半平面的垂面,则该垂面与二面角的两个半平面交线所成的角就是二面角的平面角.

三、高一数学必修2线面、面面垂直的判定大腿规律

1.直线与直线垂直

两直线垂直是指它们的交角或平移后的交角为直角，两条直线不一定相交.

在平面几何中，两直线垂直时，它们一定相交.

2.直线和平面垂直

(1)直线和平面垂直的定义可以用来判定线线垂直，即当直线和平面垂直时，该直线就垂直于这个平面内的任何直线，可以把它作为线线垂直的判定定理.

(2)要判定一条直线是否和一个平面垂直，取决于在这个平面内能否找出两条相交直线和已知直线垂直，至于这两条相交直线是否和已知直线有公共点，则无关紧要.

(3)教材中例1可以作为结论使用：

过一点和已知平面垂直的直线只有一条.

(4)如果两条直线垂直于同一个平面，则这两条直线平行，可作为两直线平行的一种判定方法.

3.(1)线面垂直的定义中的“任何一条直线”这一词语，它与“所有直线”是同义词，即直线和平面内的所有直线垂直.

(2)线面垂直的判定定理的条件中，“平面内的两条相交直线”是关键性词语，证明时一定要明确指出，弄清定理的条件是掌握好定理的关键.

(3)转化思想在本学案中的应用:

在转化时要弄清相互转化的条件，根据具体问题灵活选取恰当的证明方法.

4.证面面垂直的方法：

(1)证明两平面构成的二面角的平面角为90°.

(2)证明一个平面经过另一个平面的一条垂线，将证明“面面垂直”的问题转化为证明线面垂直的问题.

(3)证明一个平面垂直于另一个平面内的一条直线，将证明“面面垂直”的问题转化为证明“线面垂直”的问题.

5.空间中角的概念及计算是立体几何的重要内容，求角的步骤是：

(1)找出或作出有关的图形;

(2)证明它符合定义;

(3)计算.

即“一作、二证、三计算”.