七年级下册数学书第十二章习题答案
初一课程增多,同学们要如何准备呢?接下来是小编为大家带来的七年级下册数学书第十二章习题答案,供大家参考。
七年级下册数学书第十二章习题答案:
习题12.1第1题答案(2)(3)(4)是命题
(1)(5)(6)不是命题
习题12.1第2题答案(1)条件:a=c,b=c,结论:a=b
(2)条件:a<-1,结论:ab<-b
(3)条件:两直线平行,结论:内错角相等
(4)条件:一个数平方后等于4,结论:这个数是2
(5)条件:两条直线垂直于同一条直线,结论:这两条直线平行
习题12.1第3题答案(1)(3)(5)是真命题
(2)(4)是假命题
习题12.2第1题答案(1)2,3,4,32-2×4 =9 -8 =1
(2)3,4,5,42-3×5=16 -15 =1,发现这个差为1
(3)结果为1.可设中间一个数为n,则两边的数为n-1,n+1,则n2-(n-1),(n+1)=n2-(n2-1)=1
习题12.2第2题答案不是
解:设甲地到乙地全程是s km,骑自行车的速度是15 km/h,往返全程用的时间是(s/5+s/15)h,则往返全程的平均速度是:

不是步行速度的2倍
习题12.2第3题答案(1)2;E
(2)1;B
(3)AC;ED
(4)CE;AB
(5)2;A;内错角相等,两直线平行
(6)D;ACD
习题12.2第4题答案已知;2;ECD;角平分线的定义;ECD;等量代换;内错角相等,两直线平行
习题12.2第5题答案证明:∵AB∥CD(已知)
∴∠B=∠C(两直线平行,内错角相等)
∵BC∥DE(已知)
∴∠C+∠CDE=180°(两直线平行,同旁内角互补)
∴∠B+∠CDE=180°(等量代换)
习题12.2第6题答案证明:∵AD平分∠BAC(已知)
∴∠BAD=∠CAD(角平分线的定义)
∵AD∥EF(已知),∠BAD=∠AGF(两直线平行,内错角相等),∠CAF=∠F(两直线平行,同位角相等)
∴∠AGF=∠F(等量代换)
习题12.2第7题答案已知:如下图所示,直线AB、CD被直线EF所截,AB∥CD,MG平分∠BMN,NG平分/MND
求证:MG⊥NG
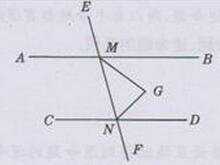
证明:∵AB∥CD(已知)
∴∠BMN+∠MND=180°(两直线平行,同旁内角互补)
∵MG平分∠BMN,NG平分∠MND(已知)
∴2∠NMG=∠BMN,2∠MNG=∠MND(角平分线的定义)
∴2∠NMG+2∠MNG=180°(等量代换),∠NMG+∠MNG=90°
又∵∠NMG+∠G+∠MNG=180°(三角形内角和定理)
∴∠G=90°
∴MG⊥NG(垂直定义)
习题12.2第8题答案证明:∵∠FEC=∠A+∠ADE,∠ABC=∠F+∠FDB(三角形的一个外角等于和它不相邻的两个内角的和),∠A=∠ABC (已知)
∴A=∠F十∠FDB(等量代换)
∵∠FDB=∠ADE(对顶角相等)
∴∠A=∠F+∠ADE(等量代换)
∴∠ADE=∠A-∠F(等式性质)
∴∠FEC=∠A+∠A-∠F(等量代换)
∴∠F+∠FEC=2∠A(等式性质)
习题12.3第1题答案(1)如果a=0,那么ab=0(原命题为假命题,逆命题为真命题)
(2)整数是自然数(原命题为真命题,逆命题为假命题)
(3)如果两个角不相等,那么这两个角就不是对顶角(原命题为假命题,逆命题为真命题)
(4)如果两个角相等,那么这两个角是内错角(原命题为假命题,逆命题为假命题)
(5)如果两个数的和为零,那么这两个数互为相反数(原命题为真命题,逆命题为真命题)
习题12.3第2题答案(1)反例:a=1,b=2,12十22≠(1+2)2
(2)反例:2是质数,但2不是奇数
(3)反例:四边形的外角和为360°,等于四边形的内角和360°
(4)反例:a=-1,b=-2,(-1-2)×[-1-(-2)]=- 3<0
习题12.3第3题答案(1)2;两直线平行,同位角相等;2;等量代换;AE;BF;同位角相等,两直线平行
(2)在(1)的推理中应用了“两直线平行,同位角相等”和“同位角相等,两直线平行”过两个互逆的真命题
习题12.3第4题答案(1)证明:∵∠B+∠1=180°(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∵∠2=∠3(已知)
∴CD∥EF(内错角相等,两直线平行)
∴AB∥EF(平行于同一条直线的两条直线平行)
∴∠B+∠F=180°(两直线平行,同旁内角互补)
(2)解在(1)的证明过程中应用了“同旁内角互补,两直线平行”和“两直线平行,同旁内角互补”这两个互逆的真命题