浅谈人力资本培训投资的博弈分析

论文关键词：投资成本 贝克尔投资模式 组合投资模式 博弈论

论文摘要：针对人力资本组合投资模式仅定性分析职员和企业对人力资本投资行为的特点，应用博弈论进行了相应的定量分析，将贝克尔投资模式与组合投资模式相结合，建立了确定企业投资比率的计算公式，为企业进行人力资本培训投资提供了定量的决策依据。

贝克尔将在职培训分为一般培训和特殊培训两种类型。一般培训是指接受培训的职工所获得的知识、技能对提高各种企业劳动生产率均有用。受训者的劳动技能提高，会提高其在各种就业机会中的工资，所以培训成本应当由受训者自巴承担。特殊培训是指接受培训的职员得到特殊知识和技能，能够极大地提高提供培训的企业的生产效率，对于提供培训以外的企业的生产效率影响不大或没有影响。特殊培训的费用较一般培训高得多，但也会给企业带来相当可观的效益，其培训成本应由企业承担。由此形成了贝克尔投资模式理论。

作为贝克尔投资模式的补充，有学者提出了一种企业和职员对人力资本共同投资的组合投资模型。该模式按照“人力资本的价值”和“人力资本的独特性”将人力资本分为四种类型：①高价值高独特性人力资本，②高价值低独特性人力资本，③低价值高独特性人力资本，④低价值低独特性人力资本。并认为①、④两种人力资本遵循贝克尔投资模式，而②、③两种人力资本则由企业和职员共同投资。组合投资模式仅在对职员和企业人力资本培训投资行为特性的分析中得出定性结论，但在企业实际经营过程中要求有定量的投资分析与决策依据。因此，本文在投资组合模式的基础上应用博弈论分析人力资本培训投资行为，找到合理且定量的组合投资分析与决策依据。

2人力资本的分类

本文仍采用人力资本培训组合投资模式中的人力资本分类方式。人力资本作为企业获取竞争优势的关键资源，并不是对企业都具有同样的重要性。

组织中的人力资本可以根据“人力资本的价值”和“人力资本的独特性”来进行划分。“人力资本的价值”是指“相对于人力资本的雇佣成本，人力资本通过其技能能够为企业带来更大的与顾客价值相关的战略利益的属性”。若职员能帮助企业降低成本或创造具有更多客户价值的产品，那他就具有高价值；反之，只有低价值。“人力资本的独特性”是指其技能的不可复制和不可模仿性。人力资本的独特性将影响到交易成本，并直接影响该人力资本能否成为企业竞争的优势源泉。由于独特技能更多地是一种适用于某一特定环境的技能，企业不可能在开放的劳动力市场上获得，对这些人力资本实行外部化将是不可行的或者将导致更多的成本，所以独特的人力资本需要进行内部开发。相反，适用于广大企业的普通技能，很容易在劳动力市场上获得，依赖于外部劳动力市场将是获得低独特性人力资本的较好选择。

按照上述两种人力资本的属性可以将企业内的人力资本分为四类：第一类人力资本具有高价值并且是独特的，即这些职员拥有特定于企业的技能，这些技能在劳动力市场上难以获得，并且职员为企业带来的战略性利益远远超过雇佣和开发他们的管理成本。也就是说，该类人力资本拥有企业竞争优势所必需的核心技能。第二类人力资本具有较高的价值，但职员拥有的技能可以在劳动力市场上获得。也就是说，其拥有的技能是低独特性的。第三类人力资本在某种程度上是独一无二的，但他们对创造客户价值并不具有直接作用。也就是说，其创造价值的能力较低或者不直接产生价值。第四类人力资本拥有普通的技能，具有有限的战略价值。以上四种人力资本类型与引言中提及的四种人力资本类型按顺序一一对应。

2人力资本培训投资选择的博弈分析

博弈论是一门研究在利益相互影响的情况下局中人(即博弈的参与者)采取何种策略才能获得最大效用的理论。博弈论在经济学、管理学等领域的应用解决了许多令经典理论无从人手的问题。博弈论最主要的特点是研究相对具体决策情况而言的最优决策，即寻找相对最满意策略而非最优策略企业和职员的人力资本培训投资选择的过程存在的正是一个博弈问题。

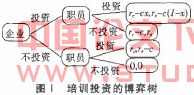
根据投资组合模型的思想，企业与职员在人力资本的投资，实际上是培训投资过程中的博弈，可以用如图1的博弈树来描述。假设企业承担培训投资成本的比率为，选择投资策略的概率为q；职员选择投资策略的概率为P。通过培训投资，企业因人力资本增加而经营效率提高所得到的利益为，职员因人力资本增加而职业生涯改善或薪酬、福利增加所获得的利益为r。为增加人力资本而进行培训投资的成本为c。按照组合投资模式的思想，企业承担的成：本为CX；职员承担的成本为c(1一)。显然，r一c>>r一c>0，1>P、q、>0。

根据子博弈均衡的逆归纳方法，只能找到一个均衡点：企业不承担培训投资成本，职员承担全部的培训投资成本。但是，如果职员是非理性的局中人，那么在企业选择不承担培训投资时，职员可能也选择不承担培训投资成本，最终使企业和职员都不获得利益。即在企业选择不投资策略时，职员可能也选择不投资策略来对企业进行威胁。由于企业选择投资策略时，职员选择不投资策略存在不承担任何培训投资成本的可能性，并且企业在利益驱动下也会对职员的威胁妥协，所以职员的这种潜在的威胁是有效的。就此而论，职员进行培训投资的概率也就是职员是否为理性的局中人的概率。如果职员是理性的，那么在获得升职、加薪或更佳的职业发展等利益的驱动下，职员将会积极地对自身的人力资本进行投资；反之，则不然。不难发现，企业投资、职员不投资与企业不投资、职员投资两种策略组合的结局，前者的结局对应贝克尔提出的特殊培训，后者的结局则对应一般培训。这与实际情况是相符的。现实情况下，企业倾向于投资具有独特性和高价值的人力资本，而职员倾向于投资具有一般性和高价值的人力资本。在企业和职员了解培训属于何种类型的情况下，他们的投资将以各自的利益为出发点，即遵循贝克尔提出的投资模式，企业承担特殊培训的全部成本，职员承担一般培训的全部成本。

然而，在不了解对方类型的情况下(包括难以归于特殊培训或一般培训的情况)，培训投资的博弈过程将如图1所示。根据图1中的博弈树可以得到：

(7)式给出了企业承担培训投资成本的比率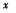的取值范围。显而易见，由于n与m的大小关系是不确定的，且只有当m>n时，(7)式才成立，所以在实际情况下企业要首先确定m与n的大小才能决定投资比率。由于企业和职员投资倾向的存在，所以可以推断P与q具有一定的关联关系，且是递减关联的。也就是说，当P(或q)增大时，q (或P)会随之减少。但是，由于企业与职员的投资决策过程相对独立，他们对投资类型的判断并不完全被对方了解，故他们的投资概率并不遵循严格的函数关系。

这就使得判断n和m的大小关系存在相当大的不确定性，即n<m是否存在是不能确定的。不过，企业对决定n与m大小关系并非无能为力，可以制定适当的投资策略(即改变q的大小)来适当改变n的大小，从而努力使得m>n成立。

那么，在满足(7)式的前提下，当P很大、q很小时。即职员倾向于投资、企业倾向于不投资时，m趋近于0，n将小于0，的取值也接近于0。这说明在这种投资情况下，企业在组合投资中承担的投资成本很少，接近于不投资。同样，当P很小、q很大时，即职员倾向于不投资、企业倾向于投资时，m趋近于无穷，n趋近于I，的取值接近于1。这说明在种投资情况下，企业在组合投资种承担的投资成本很多，接近于全部。由此可见，通过(7)式可将贝克尔投资模式和组合投资模式结合起来。

3结论

在培训投资的组合模式思想基础上，运用博弈论分析培训投资成本的组合方式，得出了关于确定企业投资比率取值范围的计算式，并将投资组合模式与贝克尔模式结合起来。因此，(7)式为企业在人力资本培训投资过程中确定投资策略和投资比率提供了决策依据。同时该式也体现了职员策略对投资比率的影响，反映出并非企业投资越多就越好。

从理论上说，(7)式的意义在于企业能对自身的投资策略作出适当的调整，找出合适的投资比率。例如，在(7)式成立的情况下，职员若不考虑自身利益有意地不选择投资策略(即降低P)，使得企业承担培训投资成本的比率上限变大，试图迫使企业承担更多的培训投资成本。此时，企业可以通过采用倾向于不投资的策略(如放弃部分利益使r减少来抵消职员行为对合作的破坏。本质上来看，这是理论上企业对职员威胁的应对策略。在决定培训投资成本各自承担的比率过程中还存在不少类似的情况。不过，职员能影响的变量只有P与r，企业能影响的变量只有q与r根据(7)式可知，当职员改变策略(即影响变量大小)试图改变不等式的取值范围时，企业都能找到抵消这种行为的影响的策略这样就能避免职员通过采取不理性策略的威胁，并规避因投资策略选择不当而产生的风险。

但应当指出，企业单方面的努力是不足以达到企业与职员共同对人力资本投资、减少接受培训职员跳槽比率的目的的。企业在进行培训投资的过程中还应对职员的投资行为进行分析，掌握职员的投资策略，才能真正做到培训投资的“双赢”。