幂函数的定义域 如何判断幂函数的定义域

一般地，形如y=x^a(a为常数)的函数，即以底数为自变量，幂为因变量，指数为常量的函数称为幂函数。如何判断幂函数的定义域?以下是小编分享给大家的关于幂函数的定义域，一起来看看吧!

幂函数的定义域

当a为不同的数值时，幂函数的定义域的不同情况如下：

1.如果a为负数，则x肯定不能为0，不过这时函数的定义域还必须根[据q的奇偶性来确定，即如果同时q为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数;2.如果同时q为奇数，则函数的定义域为不等于0 的所有实数。

判断幂函数的定义域的方法

幂函数的自变量是底数，指数是一个常数。例如x^2;定义域为底数的取值范围。

1.对于不同的指数，底数的取值范围是不同的;

2.当指数是正整数时，底数取值范围是全体实数;

3.当指数是负整数时，底数取值范围是除0外的实数，因为如果底数为0则会出现除零的错误;

4.当指数是0时，底数取值范围是除0外的实数，因为0的0次方是没有意义的。

5.当指数是正有理数时，注意到任意有理数都可以写成分数的形式，分子和分母都是正整数，当分子和分母不可约时，即它们的最大公约数是1，此时看分母的奇偶性，奇数分母的定义域是全体实数，偶数分母的定义域是非负实数， 例如x的1/2方，等于x的平方根，底数必须为正;

6.当指数是负有理数时，除了考虑指数分母的奇偶性外，还要把0剔除掉，所以应该是：奇数分母的定义域是除0外的全体实数，偶数分母的定义域是正实数。

7.当指数是正无理数时，老老实实地，定义域是 非负实数;

8.当指数是负无理数时，定义域是正实数。

幂函数的基本性质

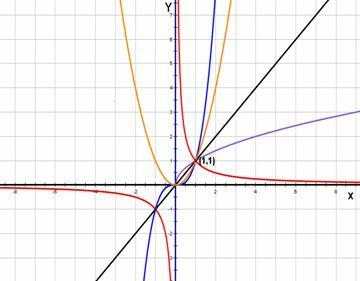
所有的幂函数在(0，+∞)上都有各自的定义，并且图像都过点(1,1)。

幂函数相关

(1)当a>0时，幂函数y=x^a有下列性质：

a、图像都通过点(1,1)(0,0) ;

b、在第一象限内，函数值随x的增大而增大;

c、在第一象限内，a>1时，图像开口向上;0