浙江高考数学考试说明(理科)
相关话题
考试是检测学生学习效果的重要手段和方法,考前需要做好各方面的知识储备。下面是小编为大家整理的浙江高考理科数学考试说明,希望对大家有所帮助!
2016年浙江省普通高考《数学(理)》考试说明
考试内容
一、集合
(一)集合的含义与表示
1.了解集合的含义、元素与集合的属于关系。
2.能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题。
(二)集合间的基本关系
1.理解集合之间包含与相等的含义,能识别给定集合的子集。
2.在具体情境中,了解全集与空集的含义。
(三)集合的基本运算
1.理解两个集合的并集与交集的含义,会求两个简单的集合的并集与交集。
2.理解在给定集合中一个子集的补集的含义,会求给定子集的补集。
3.能使用韦恩(Venn)图表示集合的关系及运算。
二、函数概念与基本初等函数Ⅰ(指数函数、对数函数、幂函数)
(一)函数
1.了解函数、映射的概念,会求一些简单的函数定义域和值域。
2.理解函数的三种表示法:解析法、图象法和列表法。
3.了解简单的分段函数,并能简单应用。
4.理解函数的单调性,会讨论和证明函数的单调性;理解函数的奇偶性,会判断函数的奇偶性。
5.理解函数的最大(小)值及其几何意义,并能求函数的最大(小)值。
6.会运用函数图象理解和讨论函数的性质。
(二)指数函数
1.了解指数函数模型的实际背景。
2.理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算。
3.理解指数函数的概念,会解决与指数函数性质有关的问题。
(三)对数函数
1.理解对数的概念及其运算性质,会用换底公式。
2.理解对数函数的概念;能解决与对数函数性质有关的问题。
(四)幂函数
(五)函数与方程
理解函数零点的概念。
(六)函数模型及其应用
1.了解指数函数、对数函数以及幂函数的变化特征。
2.能利用给定的函数模型解决简单的实际问题。
三、立体几何初步
(一)空间几何体
1.了解和正方体、球有关的简单组合体的结构特征,理解柱、锥、台、球的结构特征。
2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的直观图与三视图。
3.会用平行投影画出简单空间图形的三视图或直观图,了解空间图形的不同表示形式。
4.能识别三视图所表示的空间几何体;理解三视图和直观图的联系,并能进行转化。
5.会计算球、柱、锥、台的表面积和体积(不要求记忆公式)。
(二)点、直线、平面之间的位置关系
1.理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理。
◆公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点在此平面内。
◆公理2:过不在同一条直线上的三点,有且只有一个平面。
◆公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
◆公理4:平行于同一条直线的两条直线互相平行。
◆定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补。
2.以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定。
理解以下判定定理:
◆如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行。
◆如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行。
◆如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直。
◆如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直。
理解以下性质定理,并能够证明:
◆如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行。
◆如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行。
◆垂直于同一个平面的两条直线平行。
◆如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直。
3.理解两条异面直线所成角、直线与平面所成角、二面角的概念。
4.能证明一些空间位置关系的简单命题。
四、平面解析几何初步
(一)直线与方程
1.在平面直角坐标系中,结合具体图形,确定直线位置的几何要素。
2.理解直线的倾斜角和斜率的概念及相互间的关系,掌握过两点的直线斜率的计算公式。
3.能根据两条直线的斜率判定这两条直线平行或垂直。
4.掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系。
5.会求两直线的交点坐标。
6.掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离。
(二)圆与方程
1.掌握圆的标准方程与一般方程。
2.能判断直线与圆、圆与圆的位置关系。
3.能用直线和圆的方程解决一些简单的问题。
4.初步了解用代数方法处理几何问题。
(三)空间直角坐标系
1.了解空间直角坐标系,会用空间直角坐标表示点的位置。
2.了解空间两点间的距离公式。
五、基本初等函数Ⅱ(三角函数)
(一)角的概念、弧度制
1.了解角的概念。
2.了解弧度制的概念,能进行弧度与角度的互化。
(二)三角函数
1.理解三角函数(正弦、余弦、正切)的定义,了解三角函数的周期性。
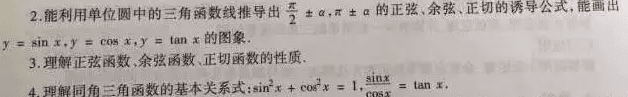
5.了解函数y = Asin(ωx+φ)的物理意义;能画出y=Asin(ωx+φ)的图象,了解参数A,ω,φ对函数图象变化的影响。
6.会用三角函数解决一些简单的实际问题。
六、平面向量
(一)平面向量的实际背景及基本概念
1.了解向量的实际背景。
2.理解平面向量的概念,理解两个向量相等的含义。
3.理解向量的几何表示。
(二)向量的线性运算
1.掌握向量加法、减法的运算,并理解其几何意义。
2.掌握向量数乘的运算及其意义,理解两个向量共线的含义。
3.了解向量线性运算的性质及其几何意义。
(三)平面向量的基本定理及坐标表示
1.理解平面向量的基本定理及其意义,会用平面向量基本定理解决简单问题。
2.掌握平面向量的正交分解及其坐标表示。
3.会用坐标表示平面向量的加法、减法与数乘运算。
4.理解用坐标表示的平面向量共线的条件。
(四)平面向量的数量积
1.理解平面向量数量积的含义及其物理意义。
2.了解平面向量的数量积与向量投影的关系。
3.掌握数量积的坐标表达式,会进行平面向量数量积的运算。
4.能运用数量积表示两个向量的夹角。
(五)向量的应用
1.会用向量方法解决某些简单的平面几何问题。
2.会用向量方法解决简单的力学问题与其他一些实际问题。
七、三角恒等变换
(一)和与差的三角函数公式
1.会用向量的数量积推导出两角差的余弦公式。
2.能利用两角差的余弦公式导出两角差的正弦、正切公式。
3.能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系。
(二)简单的三角恒等变换
能运用上述公式进行简单的恒等变换。
八、解三角形
(一)正弦定理和余弦定理
掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。
(二)应用
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
九、数列
(一)数列的概念和表示法
了解数列的概念和几种表示方法(列表、图象、通项公式)。
(二)等差数列、等比数列
1.理解等差数列、等比数列的概念。
2.掌握等差数列、等比数列的通项公式与前n项和公式。
3.了解等差数列与一次函数、等比数列与指数函数的关系。
4.能利用等差、等比数列前n项和公式及其性质求一些特殊数列的和。
5.能运用数列的等差关系或等比关系解决实际问题。
十、不等式
(一)一元二次不等式
1.会从实际情境中抽象出一元二次不等式模型。
2.了解一元二次不等式与相应的二次函数、一元二次方程的联系。
3.会解一元二次不等式。
(二)二元一次不等式组与简单线性规划问题
1.会从实际情境中抽象出二元一次不等式组。
2.了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组。
3.会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决。
(三)基本不等式:
会用基本不等式解决简单的最大(小)值问题。
十一、常用逻辑用语
1.理解必要条件、充分条件与充要条件的意义。
2.了解命题的概念,会分析原命题及其逆命题、否命题与逆否命题这四种命题的相互关系。
3.了解逻辑联结词“或”、“且”、“非”的含义。
4。 理解全称量词与存在量词的意义。
5。 能正确地对含有一个量词的命题进行否定。
十二、圆锥曲线与方程
(一)圆锥曲线
1.了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题中的作用。
2.掌握椭圆、抛物线的定义、几何图形、标准方程及简单几何性质。
3.了解双曲线的定义,掌握双曲线的几何图形和标准方程,理解它的简单几何性质。
4.能解决直线与椭圆、抛物线的位置关系等问题。
5.理解数形结合的思想。
6.了解圆锥曲线的简单应用。
(二)曲线与方程
了解方程的曲线与曲线的方程的对应关系。
十三、空间向量与立体几何
(一)空间向量及其运算
1.了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示。
2.掌握空间向量的线性运算及其坐标表示。
3.掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直。
4.掌握向量的长度公式、两向量夹角公式、空间两点间的距离公式,并会解决简单的立体几何问题。
(二)空间向量的应用
1.理解直线的方向向量与平面的法向量。
2.会用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系。
3.会用向量方法证明直线和平面位置关系的有关命题。
4.会用向量方法解决两异面直线所成角、直线与平面所成角、二面角的计算问题,了解向量方法在研究几何问题中的作用。
试卷结构
考试采用闭卷、笔试形式。考试时间120分钟。全卷满分150分。试卷包括选择题、填空题和解答题等题型。全卷共20题,其中选择题是四选一型的单选题;填空题只要求直接写出结果,不必写出计算过程或推证过程;解答题包括计算题、证明题和应用题等,解答题应写出文字说明、演算步骤和推证过程。各题型赋分如下:选择题共8小题,每小题5分,共40分;填空题共7小题,单空题每题4分,多空题每题6分,共36分;解答题共5小题,共74分。