八年级上册数学14.4课题学习习题教案
八年级的数学主要学习什么内容?上册的14.4课题主要说什么?能不能带动学生积极学习是老师的主要工作。下面是由小编整理的八年级上册数学14.4课题学习习题教案,希望对您有用。
八年级上册数学14.4课题学习习题教案篇一
◆随堂检测
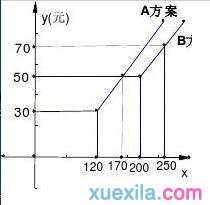
1、(2008宁波)如图,某电信公司提供了A、B两种方案的
动通讯费用y(元)与通话时间x(分)之间的关系,则以
说法错误的是( )
A.若通话时间少于120分,则A方案比B方案便宜20元
B.若通话时间超过200分,则B方案比A方案便宜12元
C.若通讯费用为60元,则B方案比A方案的通话时间长
D.若两种方案通讯费用相差10元,则通话时间是145分或185分
2、暑假老师带领该校“三好学生”去北京旅游,甲旅行社说:“若校长买全票一张,则其余学生可享受半价优惠。”乙旅行社说:“包括校长在内,全部按全票的6折优惠。”若全票为240元
①设学生数为x,甲旅行社收费为y1,乙旅行社收费为y2,则y1移下y2=
②当学生有 人时两个旅行社费用一样。
③当学生人数 时甲旅行社收费少
◆典例分析
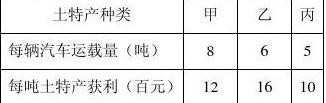
例题:某土产公司组织20辆相同型号的汽车装运甲、乙、丙三种土特产共120吨去外地销售。按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,
八年级上册数学14.4课题学习习题教案篇二
解答以下问题
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式.
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案。
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值。
分析:
(1) 装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,共20辆车,可得装运丙种土特产的车辆数为(20-x-y)辆。可得8x+6y+5(20-x-y)=120。整理成函数形式即可
(2) 由装运每种土特产的车辆都不少于3辆,可得
甲: x≥3 乙:y≥3 丙:(20-x-y)≥3
把第(1)的结论代入消去y,再解不等式即可。
(3)列出利润(因变量)与装运甲种土特产的车辆数x(自变量)的函数关系,根据函数图象的性质即可解出 解:
(1)y与x之间的函数关系式为y=20―3x
(2)由甲: x≥3 乙:y≥3 丙:(20-x-y)≥3
把y=20―3x代人
可得x≥3,y=20-3x≥3, 20―x―(20―3x)≥3 可得3x52 3
又∵x为正整数 ∴ x=3,4,5
故车辆的安排有三种方案,即:
方案一:甲种3辆 乙种11辆 丙种6辆
方案二:甲种4辆 乙种8辆 丙种8辆
方案三:甲种5辆 乙种5辆 丙种10辆
(3)设此次销售利润为W元,
W=8x·12+6(20-3x)·16+5[20-x-(20-3x)]·10
=-92x+1920
∵W随x的增大而减小 又x=3,4,5
∴ 当x=3时,W最大=1644(百元)=16.44万元
答:要使此次销售获利最大,应采用(2)中方案一,即甲种3辆,乙种11辆,丙种6辆,最大利润为16.44万元。
八年级上册数学14.4课题学习习题教案篇三
◆课下作业
●拓展提高
1、宏志中学九年级300名同学毕业前夕给灾区90名同学捐赠了一批学习用品(书包和文具盒),由于零花钱有限,每6人合买一个书包,每2人合买一个文具盒(每个同学都只参加一件学习用品的购买),书包和文具盒的单价分别是54元和12元.
(1)若有x名同学参加购买书包,试求出购买学习用品的总件数y与x之间的函数关系式(不要求写出自变量的取值范围);
(2)若捐赠学习用品总金额超过了2300元,且灾区90名同学每人至少得到了一件学习用品,请问同学们如何安排购买书包和文具盒的人数?此时选择其中哪种方案,使购买学习用品的总件数最多?
2、某学校计划租用6辆客车送一批师生参加一年一度的哈尔滨冰雕节,感受冰雕艺术的魅力.现有甲、乙两种客车,它们的载客量和租金如下表.设租用甲种客车x辆,租车总费用为y元.
(1)求出y(元)与x(辆)之间的函数关系式,指出自变量的取值范围;
(2)若该校共有240名师生前往参加,领队老师从学校预支租车费用1650元,试问预支的租车费用是否可以结余?若有结余,最多可结余多少元?
3、“六一”前夕,某玩具经销商用去2350元购进A.B.C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如右表所示,
⑴用含x、y的代数式表示购进C种玩具的套数; ⑵求y与x之间的函数关系式;
⑶假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元。
①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套。